Find the zeros of the polynomial function calculator

Mathway

Table of Contents Show

Output Type
How to find polynomial roots ?
Roots of quadratic polynomial
Quadratic equation - special cases
Roots of cubic polynomial
Cubic polynomial - factoring method
How do you find all real zeros of a function?
How do you find the zeros and roots of a polynomial function?
How do you find the missing zeros of a polynomial?

Visit Mathway on the web

Download free on Google Play

Download free on iTunes

Download free on Amazon

Download free in Windows Store

Enter a problem...

Upgrade

Calculators

About

Help

Hope that helps!

You're welcome!

Let me take a look...

You'll be able to enter math problems once our session is over.

Step-by-Step Examples

Algebra

Functions

Find the Roots (Zeros)

Step 1

Set equal to .

Step 2

Solve for .

Tap for more steps...

Use the quadratic formula to find the solutions.

Substitute the values , , and into the quadratic formula and solve for .

Simplify.

Tap for more steps...

Simplify the numerator.

Tap for more steps...

Raise to the power of .

Multiply .

Tap for more steps...

Multiply by .

Add and .

Rewrite as .

Tap for more steps...

Factor out of .

Rewrite as .

Pull terms out from under the radical.

Multiply by .

Simplify .

The final answer is the combination of both solutions.

Step 3

The result can be shown in multiple forms.

Exact Form:

Decimal Form:

Step 4

Enter YOUR Problem

About
Examples
Worksheet
Glossary
Affiliates
Careers
Press
Privacy
Terms (Premium)
Contact
DO NOT SELL MY INFO
Mathway © 2022

Mathway requires javascript and a modern browser.

EMBED

Make your selections below, then copy and paste the code below into your HTML source.
* For personal use only.

Theme

Output Type

Lightbox
Popup
Inline

Widget controls displayed
Widget results displayed

To add the widget to Blogger, click here and follow the easy directions provided by Blogger.

To add the widget to iGoogle, click here. On the next page click the "Add" button. You will then see the widget on your iGoogle account.

To embed this widget in a post on your WordPress blog, copy and paste the shortcode below into the HTML source:

For self-hosted WordPress blogs

To add a widget to a MediaWiki site, the wiki must have the Widgets Extension installed, as well as the code for the Wolfram|Alpha widget.

To include the widget in a wiki page, paste the code below into the page source.

Calculators
::
Polynomial Calculators
::
Polynomial Roots Calculator

This free math tool finds the roots (zeros) of a given polynomial. The calculator computes exact solutions for quadratic, cubic, and quartic equations.
It also displays the step-by-step solution with a detailed explanation.

Enter polynomial:

= 0

Examples:

x^2 - 4x + 3

2x^2 - 3x + 1

x^3 – 2x^2 – x + 2

EXAMPLES

find roots of the polynomial $4x^2 - 10x + 4$

find polynomial roots $-2x^4 - x^3 + 189$

solve equation $6x^3 - 25x^2 + 2x + 8 = 0$

find polynomial roots $2x^3-x^2-x-3$

find roots $2x^5-x^4-14x^3-6x^2+24x+40$

Search our database of more than 200 calculators

TUTORIAL

How to find polynomial roots ?

The process of finding polynomial roots depends on its degree. The degree is the largest exponent in the polynomial. For example, the degree of polynomial $ p(x) = 8x^\color{red}{2} + 3x -1 $ is $\color{red}{2}$.

We name polynomials according to their degree. For us, the most interesting ones are: quadratic - degree 2, Cubic - degree 3, and Quartic - degree 4.

Roots of quadratic polynomial

This is the standard form of a quadratic equation

$$ a\,x^2 + b\,x + c = 0 $$

The formula for the roots is

$$ x_1, x_2 = \dfrac{-b \pm \sqrt{b^2-4ac}}{2a} $$

Example 01: Solve the equation $ 2x^2 + 3x - 14 = 0 $

In this case we have $ a = 2, b = 3 , c = -14 $, so the roots are:

$$ \begin{aligned} x_1, x_2 &= \dfrac{-b \pm \sqrt{b^2-4ac}}{2a} \\ x_1, x_2 &= \dfrac{-3 \pm \sqrt{3^2-4 \cdot 2 \cdot (-14)}}{2\cdot2} \\ x_1, x_2 &= \dfrac{-3 \pm \sqrt{9 + 4 \cdot 2 \cdot 14}}{4} \\ x_1, x_2 &= \dfrac{-3 \pm \sqrt{121}}{4} \\ x_1, x_2 &= \dfrac{-3 \pm 11}{4} \\ x_1 &= \dfrac{-3 + 11}{4} = \dfrac{8}{4} = 2 \\ x_2 &= \dfrac{-3 - 11}{4} = \dfrac{-14}{4} = -\dfrac{7}{2} \end{aligned} $$

Quadratic equation - special cases

Sometimes, it is much easier not to use a formula for finding the roots of a quadratic equation.

Example 02: Solve the equation $ 2x^2 + 3x = 0 $

Because our equation now only has two terms, we can apply factoring. Using factoring we can reduce an original equation to two simple equations.

$$ \begin{aligned} 2x^2 + 3x &= 0 \\ \color{red}{x} \cdot \left( \color{blue}{2x + 3} \right) &= 0 \\ \color{red}{x = 0} \,\,\, \color{blue}{2x + 3} & \color{blue}{= 0} \\ \color{blue}{2x } & \color{blue}{= -3} \\ \color{blue}{x} &\color{blue}{= -\frac{3}{2}} \end{aligned} $$

Example 03: Solve equation $ 2x^2 - 10 = 0 $

This is also a quadratic equation that can be solved without using a quadratic formula.

. $$ \begin{aligned} 2x^2 - 18 &= 0 \\ 2x^2 &= 18 \\ x^2 &= 9 \\ \end{aligned} $$

The last equation actually has two solutions. The first one is obvious

$$ \color{blue}{x_1 = \sqrt{9} = 3} $$

and the second one is

$$ \color{blue}{x_2 = -\sqrt{9} = -3 }$$

Roots of cubic polynomial

To solve a cubic equation, the best strategy is to guess one of three roots.

Example 04: Solve the equation $ 2x^3 - 4x^2 - 3x + 6 = 0 $.

Step 1: Guess one root.

The good candidates for solutions are factors of the last coefficient in the equation. In this example, the last number is -6 so our guesses are

1, 2, 3, 6, -1, -2, -3 and -6

if we plug in $ \color{blue}{x = 2} $ into the equation we get,

$$ 2 \cdot \color{blue}{2}^3 - 4 \cdot \color{blue}{2}^2 - 3 \cdot \color{blue}{2} + 6 = 2 \cdot 8 - 4 \cdot 4 - 6 - 6 = 0$$

So, $ \color{blue}{x = 2} $ is the root of the equation. Now we have to divide polynomial with $ \color{red}{x - \text{ROOT}} $

In this case we divide $ 2x^3 - x^2 - 3x - 6 $ by $ \color{red}{x - 2}$.

$$ ( 2x^3 - 4x^2 - 3x + 6 ) \div (x - 2) = 2x^2 - 3 $$

Now we use $ 2x^2 - 3 $ to find remaining roots

$$ \begin{aligned} 2x^2 - 3 &= 0 \\ 2x^2 &= 3 \\ x^2 &= \frac{3}{2} \\ x_1 & = \sqrt{ \frac{3}{2} } = \frac{\sqrt{6}}{2}\\ x_2 & = -\sqrt{ \frac{3}{2} } = - \frac{\sqrt{6}}{2} \end{aligned} $$

Cubic polynomial - factoring method

To solve cubic equations, we usually use the factoting method:

Example 05: Solve equation $ 2x^3 - 4x^2 - 3x + 6 = 0 $.

Notice that a cubic polynomial has four terms, and the most common factoring method for such polynomials is factoring by grouping.

$$ \begin{aligned} 2x^3 - 4x^2 - 3x + 6 &= \color{blue}{2x^3-4x^2} \color{red}{-3x + 6} = \\ &= \color{blue}{2x^2(x-2)} \color{red}{-3(x-2)} = \\ &= (x-2)(2x^2 - 3) \end{aligned} $$

Now we can split our equation into two, which are much easier to solve. The first one is $ x - 2 = 0 $ with a solution $ x = 2 $, and the second one is $ 2x^2 - 3 = 0 $.

$$ \begin{aligned} 2x^2 - 3 &= 0 \\ x^2 = \frac{3}{2} \\ x_1x_2 = \pm \sqrt{\frac{3}{2}} \end{aligned} $$

228 328 254 solved problems

How do you find all real zeros of a function?

Graphically, the real zero of a function is where the graph of the function crosses the x‐axis; that is, the real zero of a function is the x‐intercept(s) of the graph of the function. Find the zeros of the function f ( x) = x ² – 8 x – 9. Find x so that f ( x) = x ² – 8 x – 9 = 0.

How do you find the zeros and roots of a polynomial function?

We say that x=r is a root or zero of a polynomial, P(x) , if P(r)=0 P ( r ) = 0 . In other words, x=r is a root or zero of a polynomial if it is a solution to the equation P(x)=0 P ( x ) = 0 .

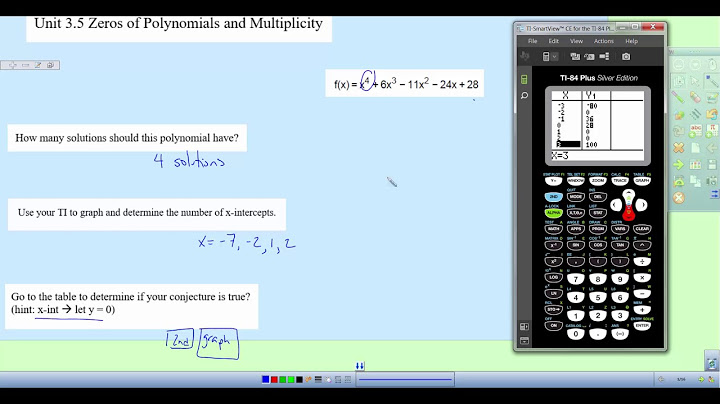
How do you find the missing zeros of a polynomial?

Use the Rational Zero Theorem to list all possible rational zeros of the function. Use synthetic division to evaluate a given possible zero by synthetically dividing the candidate into the polynomial. If the remainder is 0, the candidate is a zero. If the remainder is not zero, discard the candidate.